ai学习:卷积与池化
从全连接层到卷积层
全连接层主要进行矩阵乘法(线性变换),其当前层的所有神经元,都与上一层的所有神经元相连,主要用于特征整合、样本映射等。数学表达如下:
\[y = \sigma(W \cdot x + b)\]但是对于图像识别来说,全连接层有着诸多的不足。 假设一个 $1000 \times 1000$ 像素的图片,输入维度就有 $1000 \times 1000$,假设下一层 $1,000$ 个神经元,那么参数就有 $1000 \times 1000 \times 1000$,10 亿个参数,这还只是一层。 从另一个角度来说,人们从图像中识别特定物体时,目标物体是否能被识别,只取决于物体的局部特征的上下文信息,而与其位置、缩放、旋转、光照、是否被部分遮挡、一定的形变等无关。计算机视觉 (computer vision, CV) 网络架构也应支持这种不变性,只要物体保留了大部分局部特征,基于前几层的局部感受野和权重共享机制,算法都能产生一致性的响应输出。所以我们需要捕捉局部空间的特征,而全连接层是很难获得空间特征的。
适合于计算机视觉的神经网络架构应有以下特点:
- 平移不变性(translation invariance):不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”。
- 局部性(locality):神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是“局部性”原则。最终,可以聚合这些局部特征,以在整个图像级别进行预测。
推导
从多层感知机 MLP 开始,输入是二维图像 X,隐藏表示 H 与 X 有相同的形状,保证图像中[X]i,j 与[H]i,j 一一对应。
为了考虑像素间的空间结构与相对位置关系,用每个像素点的位置(k,l)加权隐藏表示中各神经元的位置(i,j)得到新的四阶权重张量[W]i,j,k,l。隐藏层处的神经元激活值的数学表示如下:
\[[\mathbf{H}]_{i,j} = \sum_{k} \sum_{l} [\mathbf{W}]_{i,j,k,l} [\mathbf{X}]_{k,l} + [\mathbf{U}]_{i,j}\][X]k,l:输入图像处的像素值;
- [W]i,j,k,l:与隐藏层神经元位置权重连接后的新的权重;
- $\sum_{k} \sum_{l}$:加权求和图像的所有像素位置;
- [U]i,j:隐藏层处的偏置项。
为了将像素位置(k,l)用相对于(i,j)的偏移量表示,令 k=i+a、l=j+b。于是[W]i,j,k,l 被重新表示为 Vi,j,a,b。隐藏层处的神经元激活值可继续用新的形式表示为:
\[[\mathbf{H}]_{i,j} = \sum_{a} \sum_{b} [\mathbf{V}]_{i,j,a,b} [\mathbf{X}]_{i+a, j+b} + [\mathbf{U}]_{i,j}\]又由于平移不变性,位置参数 i、j 与隐藏层(i,j)处的神经元激活值无关,故:
\[[\mathbf{H}]_{i,j} = \sum_{a} \sum_{b} [\mathbf{V}]_{a,b} [\mathbf{X}]_{i+a, j+b} + u\]最后,基于局部性基本原理,神经元只需要每次关注输入图像的局部区域,而不是整个图像。为此,引入一个距离参数 $\Delta$。当偏移量超过 $\Delta$,即 $a>\Delta$ 或 $b>\Delta$ 时,超过部分的像素对当前神经元的计算无影响, Va,b=0。这样,隐藏层(i,j)处的神经元激活值可继续表示为:
\[[\mathbf{H}]_{i,j} = \sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta} [\mathbf{V}]_{a,b} [\mathbf{X}]_{i+a, j+b} + u\]卷积
简单实现
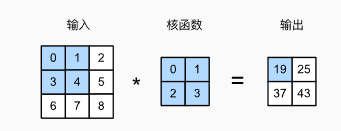
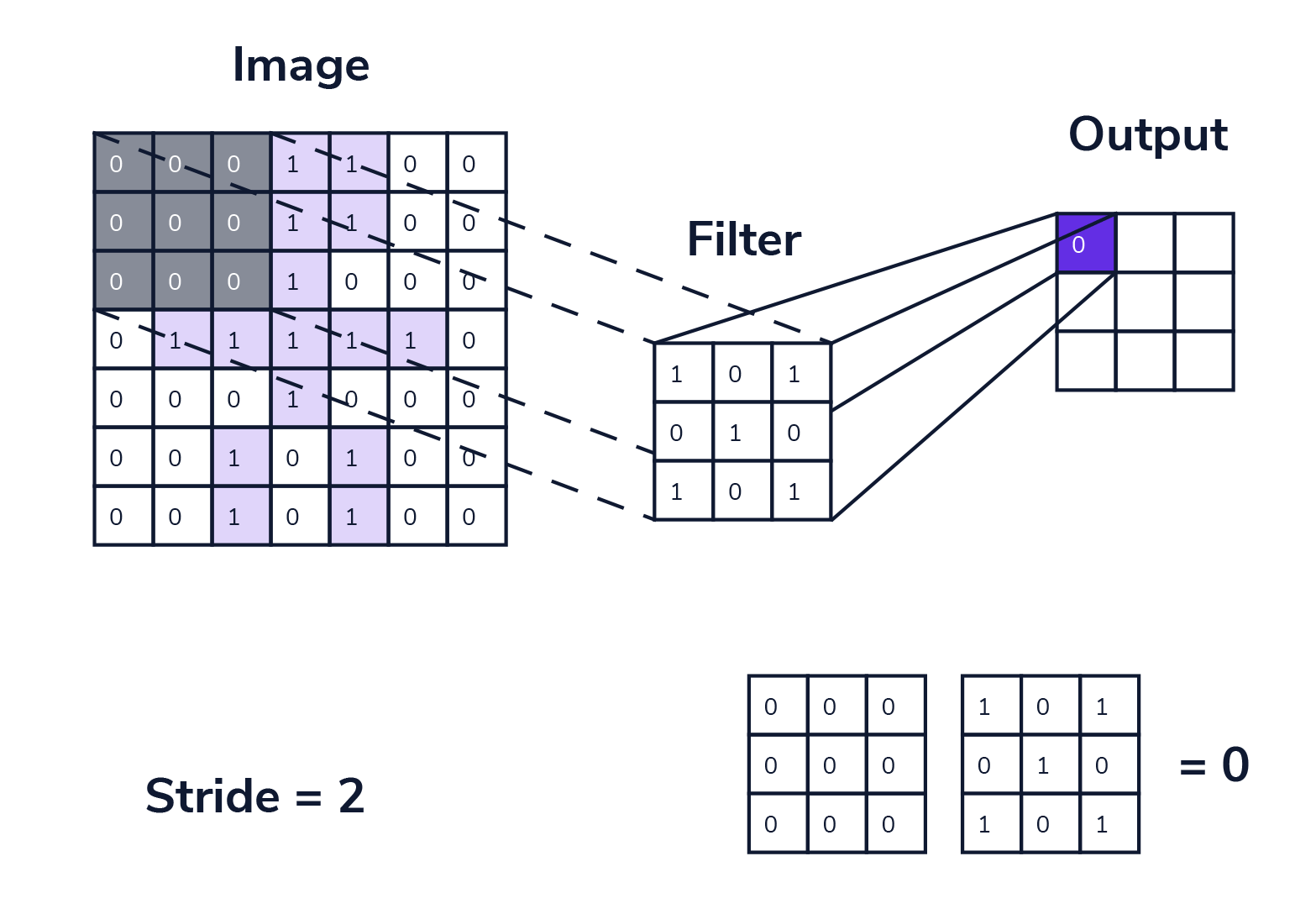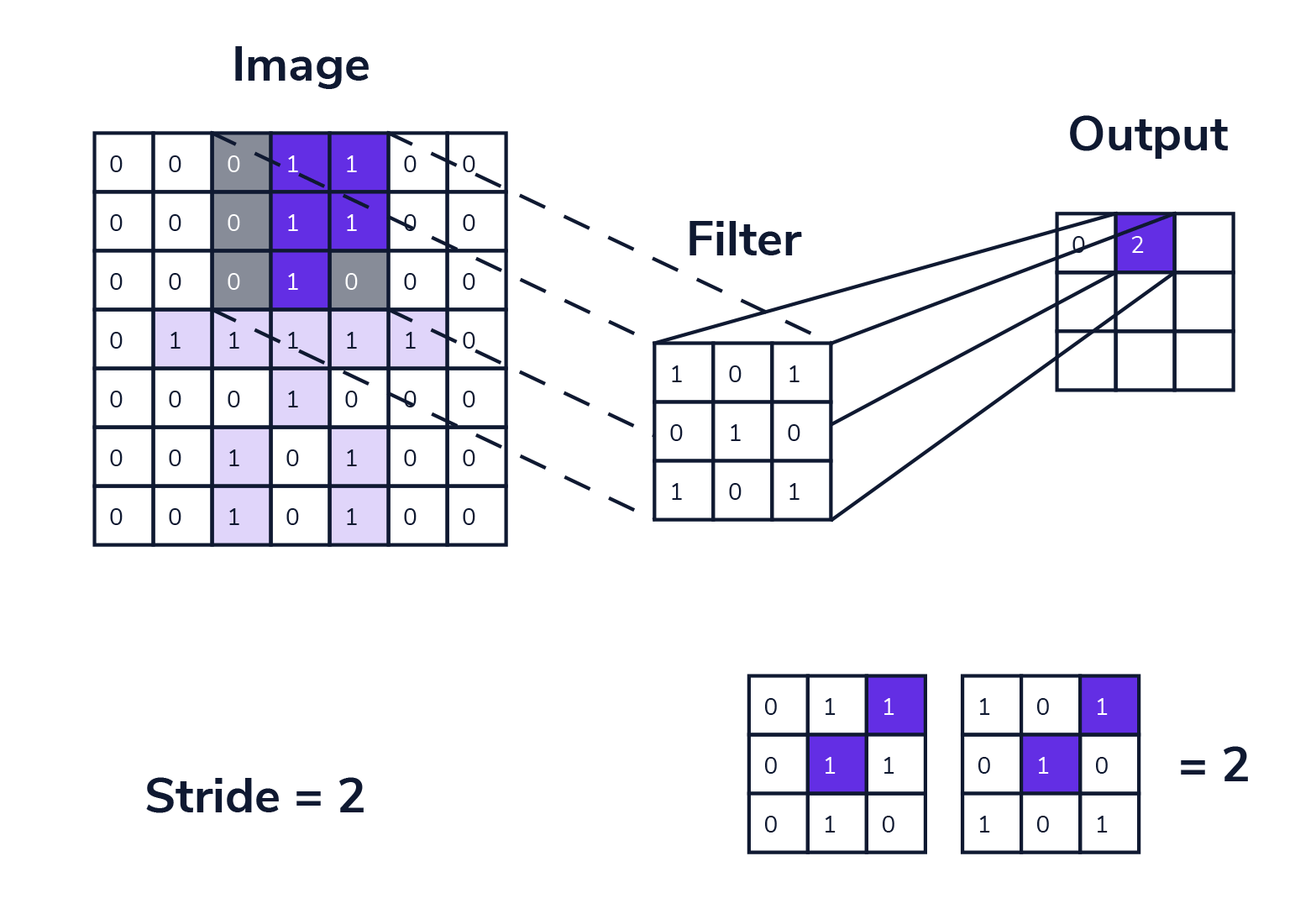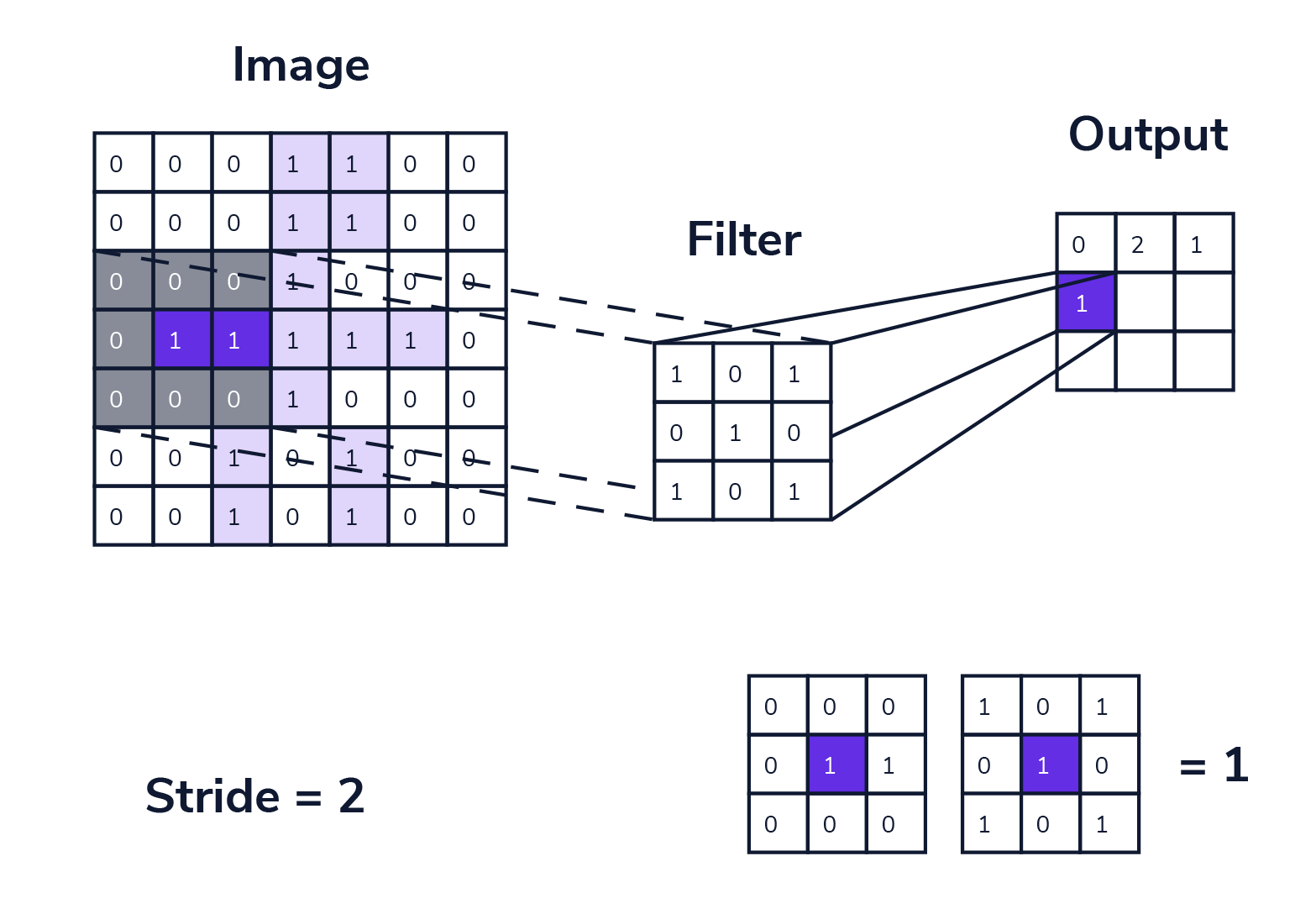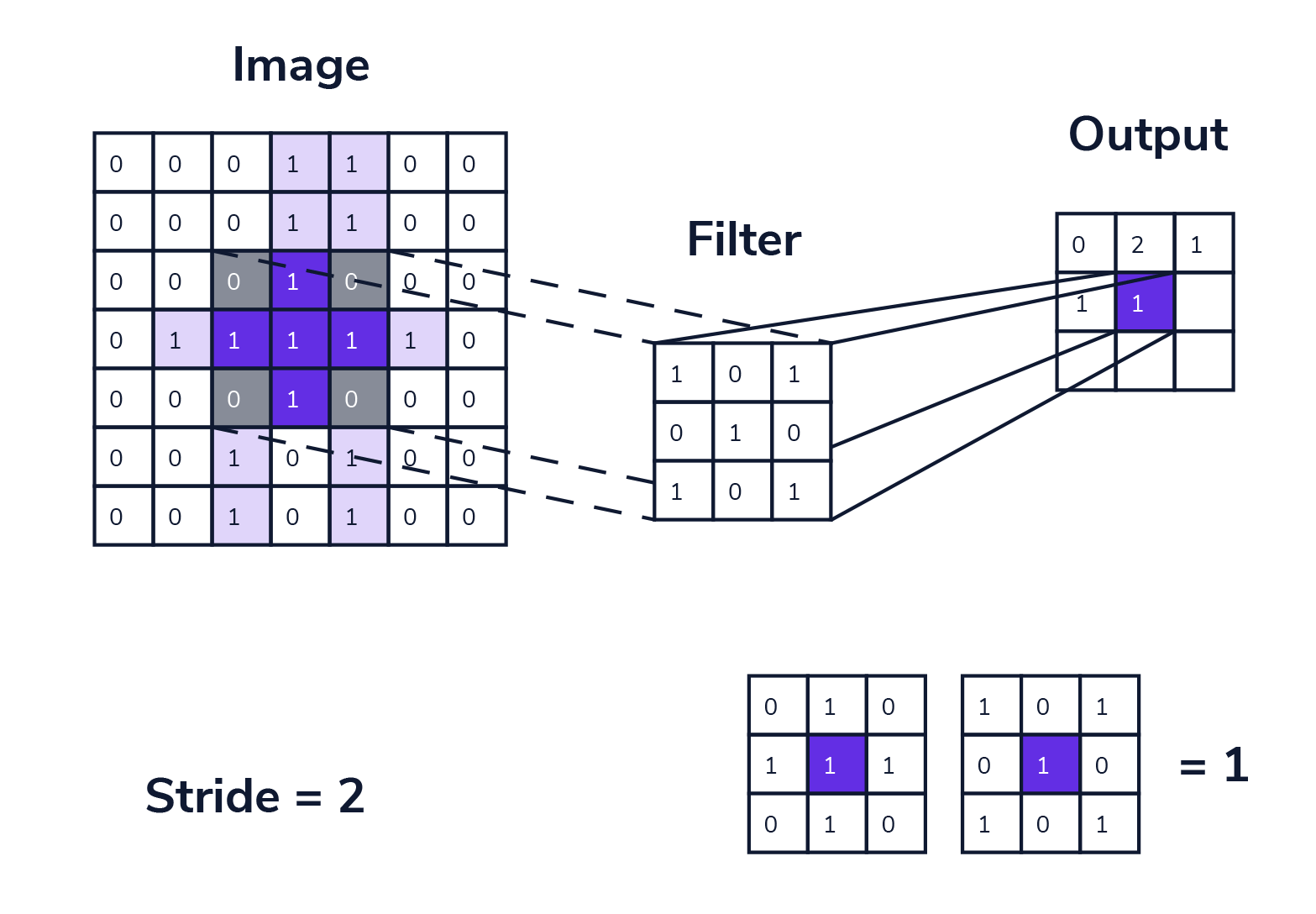
用一个图来表示卷积的操作:
简单来说就是不断的使用卷积核在图像上进行滑动,从而捕捉图像局部的特征。代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import torch
from torch import nn
def corr2d(X,K): #X为输入,K为核矩阵
h,w=K.shape #h得到K的行数,w得到K的列数
Y=torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1)) #用0初始化输出矩阵Y
for i in range(Y.shape[0]): #卷积运算
for j in range(Y.shape[1]):
# 输入的局部区域与卷积核的逐元素相乘,并求和
Y[i,j]=(X[i:i+h,j:j+w]*K).sum()
return Y
#样例点测试
X=torch.tensor([[0,1,2],[3,4,5],[6,7,8]])
K=torch.tensor([[0,1],[2,3]])
corr2d(X,K)
1
2
tensor([[19., 25.],
[37., 43.]])
边界检测中应用
图像边缘本质上是图像像素值发生变化的位置,可以用互相关运算检测。
这里给出一个示例:对于一幅像素尺寸为 6×8 的黑白图像,用 1 表示白色,用 0 表示黑色,使用水平差分算子检测水平方向的边缘(亦可选择其他类型的算子检测其他方向的边缘)。
下面先初始化图像:
1
2
3
X=torch.ones((6,8))
X[:,2:6]=0
X
1
2
3
4
5
6
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
下面是一个简单的边界检测的核函数:
1
2
3
K=torch.tensor([[-1,1]]) #这个K只能检测垂直边缘
Y=corr2d(X,K)
Y
1
2
3
4
5
6
tensor([[ 0., -1., 0., 0., 0., 1., 0.],
[ 0., -1., 0., 0., 0., 1., 0.],
[ 0., -1., 0., 0., 0., 1., 0.],
[ 0., -1., 0., 0., 0., 1., 0.],
[ 0., -1., 0., 0., 0., 1., 0.],
[ 0., -1., 0., 0., 0., 1., 0.]])
卷积层
卷积层对输入数据与卷积核执行互相关运算并滑动,添加偏置项后生成特征图(也称为特征映射)。其中,特征图的维数等于卷积层的输出通道数 out_channels。卷积核权重的学习过程,就是从输入数据提取边缘、纹理或形状等特征的过程。 在实现卷积层时,与全连接层的实现类似,同样需要定义权重 weight 和偏置 bias 2 个参数:
1
2
3
4
5
6
7
8
#实现二维卷积层
class Conv2d(nn.Module):
def _init_(self,kernel_size):
super()._init_()
self.weight=nn.Parameter(torch.rand(kerner_size))
self.bias=nn.Parameter(torch.zeros(1))
def forward(self,x):
return corr2d(x,self.weight)+self.bias
学习卷积核
在上面的边界检测中我们直接指定了用于检测水平黑白边缘的卷积核,并很有效。但在更复杂的场景下,希望能“学习到”适合特定模式的卷积核。 于是,在卷积层中将卷积核初始化为随机张量,用深度学习的思想更新卷积核(忽略偏置):
1
2
3
4
5
6
7
8
9
10
11
12
13
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat - Y)**2
conv2d.zero_grad()
l.sum().backward()
conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f'batch {i+1}, loss {l.sum():.3f}')
1
2
3
4
5
batch 2, loss 11.679
batch 4, loss 2.061
batch 6, loss 0.387
batch 8, loss 0.082
batch 10, loss 0.021
根据结果,这种方法可以有效地“学习”到目标卷积核[[1,-1]]
特征映射和感受野
输出的卷积层有时被称为特征映射(feature map),因为它可以被视为一个输入映射到下一层的空间维度的转换器。 在卷积神经网络中,对于某一层的任意元素 x,其感受野(receptive field)是指在前向传播期间可能影响计算的所有元素(来自所有先前层)。
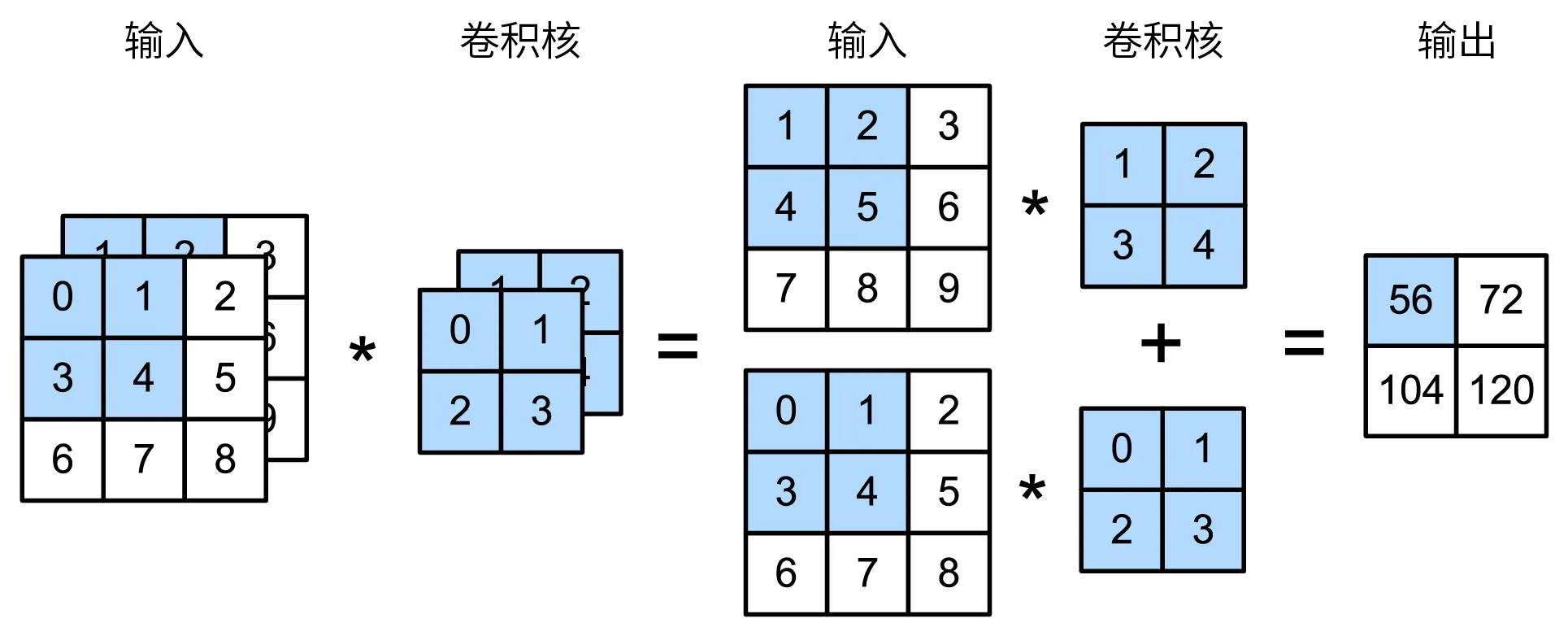
让我们用卷积小节第一张图为例来解释感受野: 给定 $2\times2$ 卷积核,阴影输出元素值 19 的感受野是输入阴影部分的四个元素。 假设之前输出为 Y,其大小为 $2\times2$,现在我们在其后附加一个卷积层,该卷积层以 Y 为输入,输出单个元素 z。 在这种情况下,Y 上的 z 的感受野包括 Y 的所有四个元素,而输入的感受野包括最初所有九个输入元素。 因此,当一个特征图中的任意元素需要检测更广区域的输入特征时,我们可以构建一个更深的网络。
填充与步幅
有时,在应用了连续的卷积之后,我们最终得到的输出远小于输入大小。这是由于卷积核的宽度和高度通常大于 1 所导致的。比如,一个 $240\times240$ 像素的图像,经过 10 层 $5\times5$ 的卷积后,将减少到像素 $200\times200$。如此一来,原始图像的边界丢失了许多有用信息,而填充是解决此问题最有效的方法; 有时,我们可能希望大幅降低图像的宽度和高度。例如,如果我们发现原始的输入分辨率十分冗余。步幅则可以在这类情况下提供帮助。
填充
填充即是在边界再进行扩展边界,根据卷积操作后,输入输出尺寸的变化,填充的类型可分为:
- 有效填充 (valid padding) :
边界处的像素不被填充扩展,卷积核只能在图像内部滑动。输出尺寸小于输入尺寸。
- 同维填充 (same padding) :
填充以扩展边界,使输出尺寸与输入尺寸相同。输出尺寸等于输入尺寸。
- 完全填充 (full padding) :
向边界填充更多的像素,使卷积核覆盖整个输入图像(包括边界外的部分)。输出尺寸大于输入尺寸。
大多数情况,默认使用 0 填充边界。亦可使用边界处像素的镜像填充边界。实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import torch
import torch.nn as nn
i = torch.randn(1, 1, 13, 13) # (批量大小, 通道数, 高度, 宽度)
i_size = torch.tensor(i.shape[-2:])
IN_CHANNELS = 1
OUT_CHANNELS = 1
KERNEL_SIZE = 3
STRIDE = 1
padding_vali = 0
padding_same = ((i_size - 1) * STRIDE + KERNEL_SIZE - i_size) // 2
padding_full = ((STRIDE - 1) * i_size + (STRIDE + 1) * KERNEL_SIZE - 2 * STRIDE) // 2
o_vali = nn.Conv2d(IN_CHANNELS, OUT_CHANNELS, KERNEL_SIZE, STRIDE, padding_vali)(i) # padding='valid'
o_same = nn.Conv2d(IN_CHANNELS, OUT_CHANNELS, KERNEL_SIZE, STRIDE, padding_same)(i) # padding='same'
o_full = nn.Conv2d(IN_CHANNELS, OUT_CHANNELS, KERNEL_SIZE, STRIDE, padding_full)(i)
print(f'{i.shape = }')
print(f'{o_vali.shape = }')
print(f'{o_same.shape = }')
print(f'{o_full.shape = }')
1
2
3
4
i.shape = torch.Size([1, 1, 13, 13])
o_vali.shape = torch.Size([1, 1, 11, 11])
o_same.shape = torch.Size([1, 1, 13, 13])
o_full.shape = torch.Size([1, 1, 15, 15])
步幅
步幅 (stride) 是卷积层中的另一个重要参数,决定了卷积核在输入数据从左上角向右下角每次向下、向右滑动经过的像素数量。
步幅越大,输出的尺寸越小,降低了特征图的分辨率,也减少了计算量和内存消耗,有助于去冗余和提取更高层次的特征。
实现也很简单,nn.Conv2d(IN_CHANNELS, OUT_CHANNELS, KERNEL_SIZE, STRIDE, padding_vali)(i) 中 STRIDE 即为该超参数。
多通道输入输出
通道 (channel) 主要用于表示数据的维度。如:
- 图像数据:RGB 图像有红、绿、蓝三种颜色通道,灰度或黑白图像只有一个表示亮度的通道;
- 音频数据:立体声的音频数据有左、右两个声音通道,环绕立体声的音频数据有更多的通道。当音频数据用频谱图 (spectrogram) 表示时,每个频率分量对应一个通道;
- 时序数据:每个传感器单元捕获的数据可分别看作一个通道。
先前的案例只使用了一个通道演示,但更多的情况是以 RGB 的色彩模式处理图像数据的。于是,需要在卷积操作时考虑数据维度为 $c\times h\times w$ 的情况。
多通道输入
为了分别在各个通道上执行卷积(互相关)操作,当数据以多通道的形式输入时,卷积核的通道数应与输入数据的通道数一致。这样,计算得到 3 维结果的形状为 $c_{in} \times h’ \times w’$。为了保证每个卷积核只生成一个 2 维的特征图,需要将 3 维结果中的每个通道按元素求和后输出。下面是一个双通道输入的例子:
代码实现:
1
2
3
def corr2d_multi_in(X, K):
# 先遍历“X”和“K”的第0个维度(通道维度),再把它们加在一起
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
多通道输出
到目前为止,不论有多少输入通道,我们还只有一个输出通道。但是在最流行的神经网络架构中,随着神经网络层数的加深,我们常会增加输出通道的维数,通过减少空间分辨率以获得更大的通道深度。直观地说,我们可以将每个通道看作对不同特征的响应。而现实可能更为复杂一些,因为每个通道不是独立学习的,而是为了共同使用而优化的。因此,多输出通道并不仅是学习多个单通道的检测器。
用 ci 和 co 分别表示输入和输出通道的数目,并让 kh 和 kw 为卷积核的高度和宽度。为了获得多个通道的输出,我们可以为每个输出通道创建一个形状为 $c_i\times k_h\times k_w$ 的卷积核张量,这样卷积核的形状是 $c_o\times c_i\times k_h\times k_w$。在互相关运算中,每个输出通道先获取所有输入通道,再以对应该输出通道的卷积核计算出结果。
代码实现:
1
2
3
4
5
6
7
8
9
def corr2d_multi_in_out(X, K):
# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。
# 最后将所有结果都叠加在一起
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
K = torch.stack((K, K + 1, K + 2), 0) #构造一个多输出通道的卷积核
K.shape
corr2d_multi_in_out(X, K)
1
2
3
4
5
6
7
8
9
10
torch.Size([3, 3, 3, 2, 2, 2])
tensor([[[ 56., 72.],
[104., 120.]],
[[ 76., 100.],
[148., 172.]],
[[ 96., 128.],
[192., 224.]]])
1×1 卷积层
当卷积层的卷积核尺寸为 1×1 时,该卷积层被称为 1×1 卷积层。这样的卷积层失去了识别宽高维临近像素间特征的能力,但能继续操作通道,在调整复杂深层网络的通道维度、整合特征和降低计算复杂度等方面很流行。
以 3 通道输入、2 通道输出的 1×1 卷积层,计算示意图如下:
1×1 卷积层的主要作用如下:
- 降维与升维:在不改变输出的空间维度前提下,调整卷积核数量改变输出通道数,实现降维与升维。可以在处理较大卷积核时作为“瓶颈层”,减小计算量或提高模型的表达能力;
- 线性组合通道信息:通过对每个像素位置的通道值加权求和,(与全连接层类似,)实现通道间的线性组合;
- 增加非线性特征的表达能力:与非线性激活函数(如 ReLU)联用后,能使增加网络的非线性特征表达能力。
下面我们使用全连接层实现 1x1 卷积(ai 加注释):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def corr2d_multi_in_out_1x1(X, K):
c_i, h, w = X.shape
c_o = K.shape[0] # 输出通道数
# [关键步骤 1] 拉平空间维度
# 把 (通道, 高, 宽) 变成 (通道, 像素总数)
# 也就是把整张图的所有像素排成一排,但保留通道结构
X = X.reshape((c_i, h * w))
# [关键步骤 2] 压缩卷积核
# 原始 K 是 (c_o, c_i, 1, 1),最后两个维度是 1,直接去掉
# 变成 (输出通道, 输入通道),这就是全连接层的权重矩阵 W
K = K.reshape((c_o, c_i))
# [关键步骤 3] 矩阵乘法 (全连接操作)
# (c_o, c_i) 乘以 (c_i, h*w) -> 得到 (c_o, h*w)
# 这相当于对每一个像素点(共 h*w 个)都做了一次独立的全连接计算
Y = torch.matmul(K, X)
# [关键步骤 4] 恢复形状
# 把拉平的像素 (h*w) 重新还原成 (h, w)
return Y.reshape((c_o, h, w))
池化层
像素矩阵输入到卷积层,与卷积核进行互相关运算后,由局部感受野提取局部特征(如边缘、纹理等),保留了输入数据的空间结构。但计算机视觉任务的决策基于图像全局,而不是局部特征。
因此,若能在处理图像时,以某种方式实现降采样(降低隐藏表示的空间分辨率)、汇聚信息,局部感受野的范围将随着层的叠加而逐渐扩展,使网络最终生成对全局敏感的表示。池化层 (pooling layer) 在卷积神经网络中发挥了重要的作用,旨在促进网络更好地学习抽象特征:
- 对特征图进行下采样,减少其空间维度、降低模型复杂度,减小计算量和过拟合风险;
- 提取特征中最显著的关键部分而去掉不必要的细节,使特征对微小的空间变动具有更好的不变性。
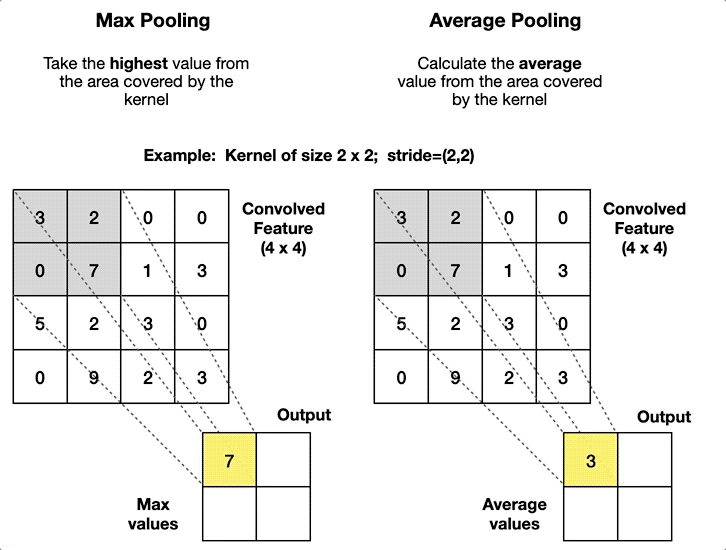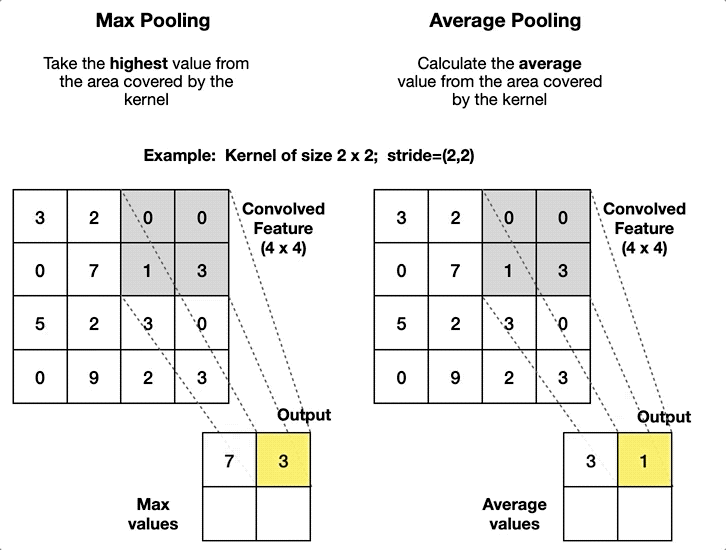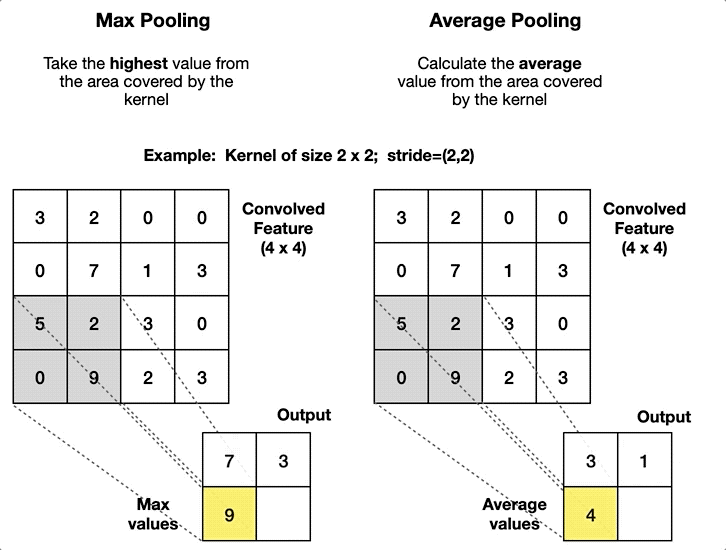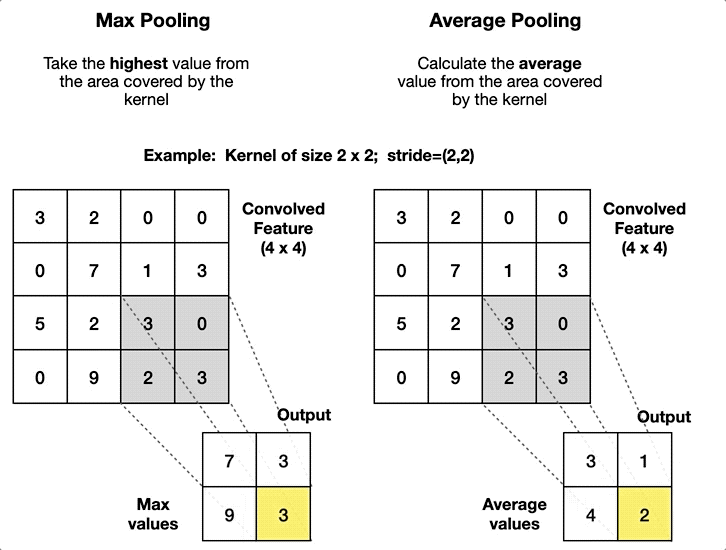
与卷积层的感受野类似,池化层使用池化窗口 (pooling window) 限制降采样过程中区域的大小和形状。根据降采样实现的方式,池化层有 2 种常见类型:
- 最大池化 (max-pooling) 层:汇聚将每个池化窗口的最大值作为新的特征图;
- 平均池化 (average-pooling) 层:汇聚将每个池化窗口的平均值作为新的特征图。
代码实现也很简单:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
from torch import nn
from d2l import torch as d2l
def pool2d(X, pool_size, mode='max'):
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y
使用 pytorch 框架时:
1
pool2d = nn.MaxPool2d(3, padding=1, stride=2)